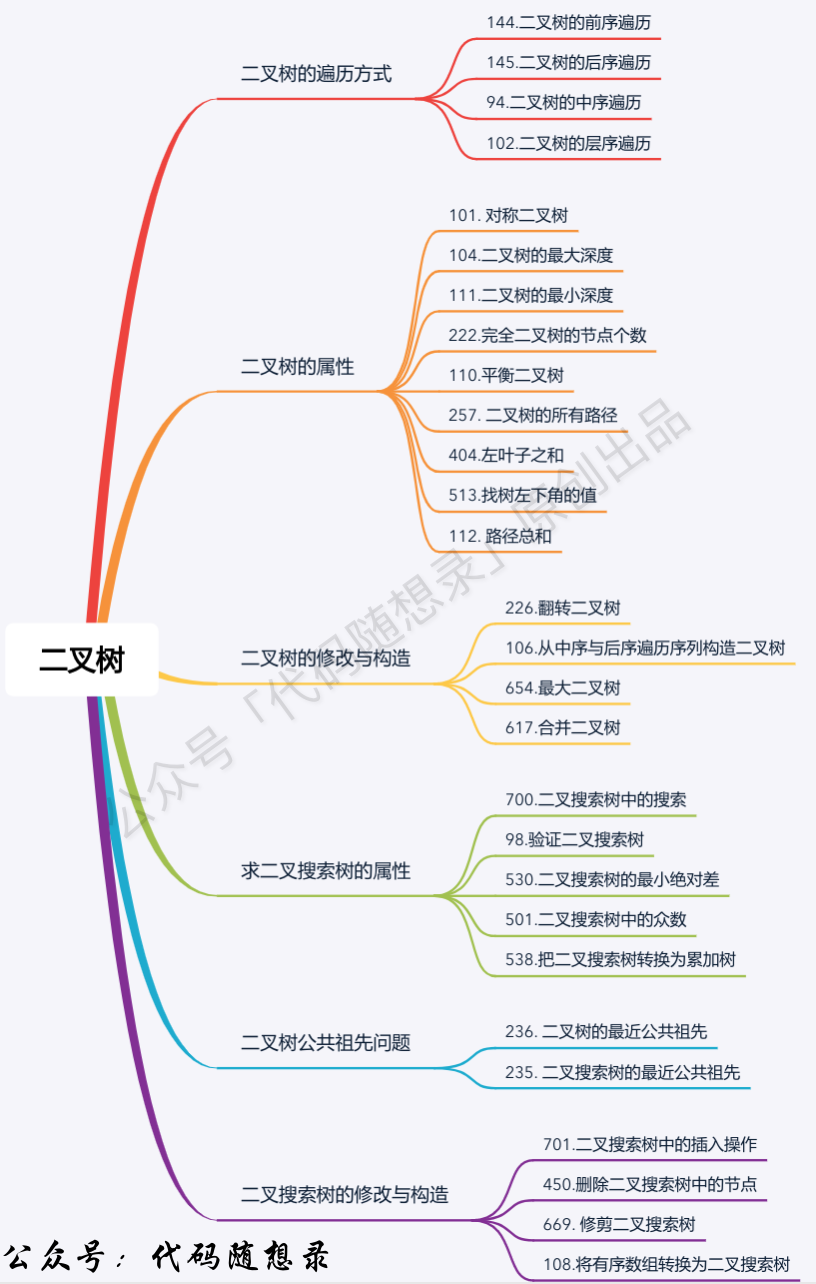
二叉树理论基础
##二叉树的种类
- 满二叉树:一颗二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则二叉树为满二叉树
深度为K,有2^(k) - 1个节点的二叉树
完全二叉树,除了最底层结点可能没填满外,其余每层节点数都达到最大值,且最下面一层的结点都集中在该层最左边的若干位置
二叉搜索树,是一个有序树
若左子树不空,则左子树上所有结点值均小于根节点的值
若右子树不空,则右子树上所有结点值均大于根节点的值
即他的左子树和右子树也分别为二叉搜索树
平衡二叉搜索树
它是一颗空树,或他的左右两个子树的高度差的绝对值不超过一,并且左右两个子树都是一颗平衡二叉树
二叉树的存储方式
二叉树可以链式存储,也可以顺序存储
链式:用指针
指针存储就是,节点值和左指针,右指针的值
顺序:用数组
数组存储遍历模式,如果父节点是i,左节点即为2*i + 1,右节点即为 2 * i+ 2
二叉树的遍历方式
深度优先遍历
先往深走,遇到叶子结点再往回走
前中后的区别是中间节点的遍历顺序
- 前序遍历
中左右
- 中序遍历
左中右
- 后序遍历
左右中
借助栈使用递归的方式实现
广度优先遍历
一层一层的遍历
层次遍历
借助队列实现一层一层遍历
二叉树的定义
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public class TreeNode{
int val;
TreeNode left;
TreeNode right;
TreeNode(){}
TreeNode(int val){ this.val = val;}
TreeNode(int val, TreeNode left, TreeNode right){
this.val = val;
this.left = left;
this.right = right;
}
}
|
二叉树的递归遍历
递归三要素
- 确定递归函数的参数和返回值
- 确定终止条件
- 确定单层递归逻辑
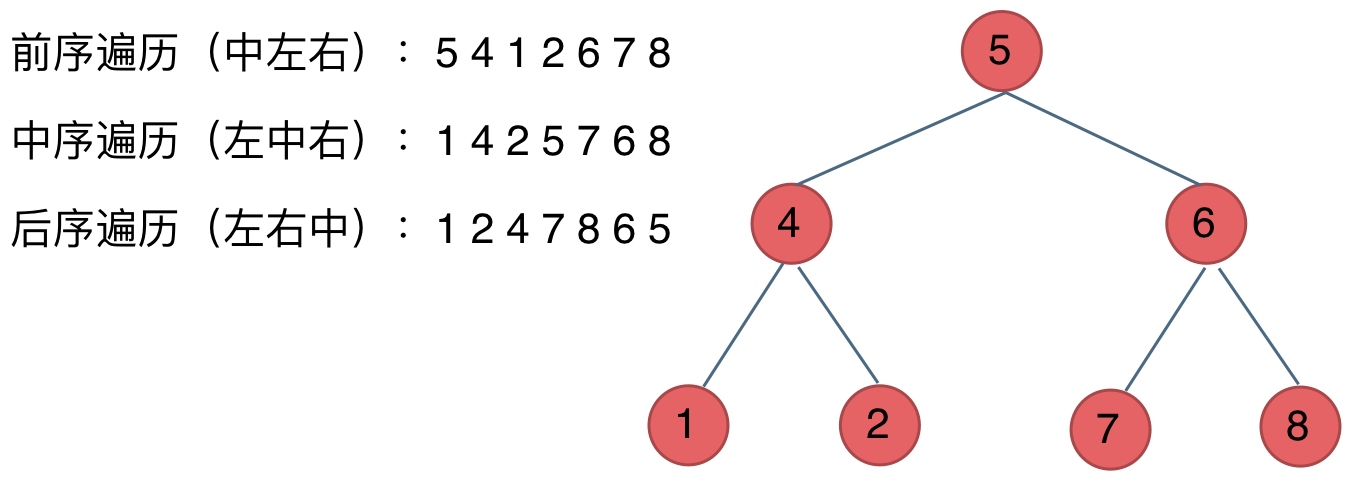
144 二叉树的前序遍历
牢记前序遍历的顺序为 中 - 左 - 右
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution{
public List<Integer> preorderTraversal(TreeNode root){
List<Integer> result = new ArrayList<>();
preorder(root, result);
return result;
}
public void preorder(TreeNode root, List<Integer> result){
if (root == null) return;
result.add(root.val);
preorder(root.left, result);
preorder(root.right, result);
}
}
|
145 二叉树的后序遍历
后序遍历的顺序为 左 - 右 - 中左右
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
postorder(root, result);
return result;
}
public void postorder(TreeNode root, List<Integer> result){
if (root == null) return;
postorder(root.left, result);
postorder(root.right, result);
result.add(root.val);
}
}
|
94 二叉树的中序遍历
中序遍历的顺序是 左 - 中 - 右指针的值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
inorder(root, result);
return result;
}
public void inorder(TreeNode root, List<Integer> result){
if (root == null) return;
inorder(root.left, result);
result.add(root.val);
inorder(root.right, result);
}
}
|
二叉树的迭代遍历
递归的实现就是:每一次递归调用都会把函数的局部变量,参数值和返回地址压入调用栈中
由此 前中后序遍历也可使用栈进行遍历
前序遍历
前序遍历是中 - 左 - 右
现将根节点放入栈中,然后把右孩子加入栈,再讲左孩子加入栈
现将root节点放入,之后把root节点值输出之后,先判断右边,再判断左边,之后循环这一个过程,直到栈空
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
class Solution{
public List<Integer> preorderTraversal(TreeNode root){
List<Integer> result = new ArrayList<>();
if (root == null){
return result;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()){
TreeNode node = stack.pop();
result.add(node.val);
if (node.right != null){
stack.push(node.right);
}
if (node.left != null){
stack.push(node.left);
}
}
return result;
}
}
|
中序遍历
使用迭代法写中序遍历时,用指针遍历访问节点,用栈处理节点上的元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution{
public List<Integer> inorderTraversal(TreeNode root){
List<Integer> result = new ArrayList<>();
if (root == null) return result;
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()){
if (cur != null){
stack.push(cur);
cur = cur.left;
} else {
cur = stack.pop();
result.add(cur.val);
cur = cur.right;
}
}
return result;
}
}
|
后序遍历
前序遍历先把左右调换顺序之后把result数组反过来就可以成为后序遍历的顺序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution{
public List<Integer> postorderTraversal(TreeNode root){
List<Integer> result = new ArrayList<>();
if (root == null) return result;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()){
TreeNode node = stack.pop();
result.add(node.val);
if (node.left != null) stack.push(node.left);
if (node.right != null) stack.push(node.right);
}
Collections.reverse(result);
return result;
}
}
|
二叉树的统一迭代
以中序遍历为例,无法同时解决访问节点和处理节点不一致的情况
此时,把访问节点放入栈中,把要处理的结点也放入栈中在处理节点之后放入空指针作为标记
即读到null后,跳两格读数,因为顺序在之前已经写好了,只需要处理读数问题
前序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
class Solution{
public List<Integer> preorderTraversal(TreeNode root){
List<Integer> result = new ArrayList<>();
if (root == null) return result;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()){
TreeNode node = stack.peek();
if (node != null){
stack.pop();
if (node.right != null) stack.push(node.right);
if (node.left != null) stack.push(node.left);
stack.push(node);
stack.push(null);
} else {
stack.pop();
node = stack.pop();
result.add(node.val);
}
}
return result;
}
}
|
中序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) return result;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()){
TreeNode node = stack.peek();
if (node != null){
stack.pop();
if (node.right != null) stack.push(node.right);
stack.push(node);
stack.push(null);
if (node.left != null) stack.push(node.left);
} else {
stack.pop();
node = stack.peek();
stack.pop();
result.add(node.val);
}
}
return result;
}
}
|
后序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
class Solution{
public List<Integer> postorderTraversal(TreeNode root){
List<Integer> result = new ArrayList<>();
if (root == null) return result;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()){
TreeNode node = stack.peek();
if (node != null){
stack.pop();
stack.push(node);
stack.push(null);
if (node.right != null) stack.push(node.right);
if (node.left != null) stack.push(node.left);
} else {
stack.pop();
result.add(stack.pop().val);
}
}
return result;
}
}
|

