代码随想录第十七天

Posted on In

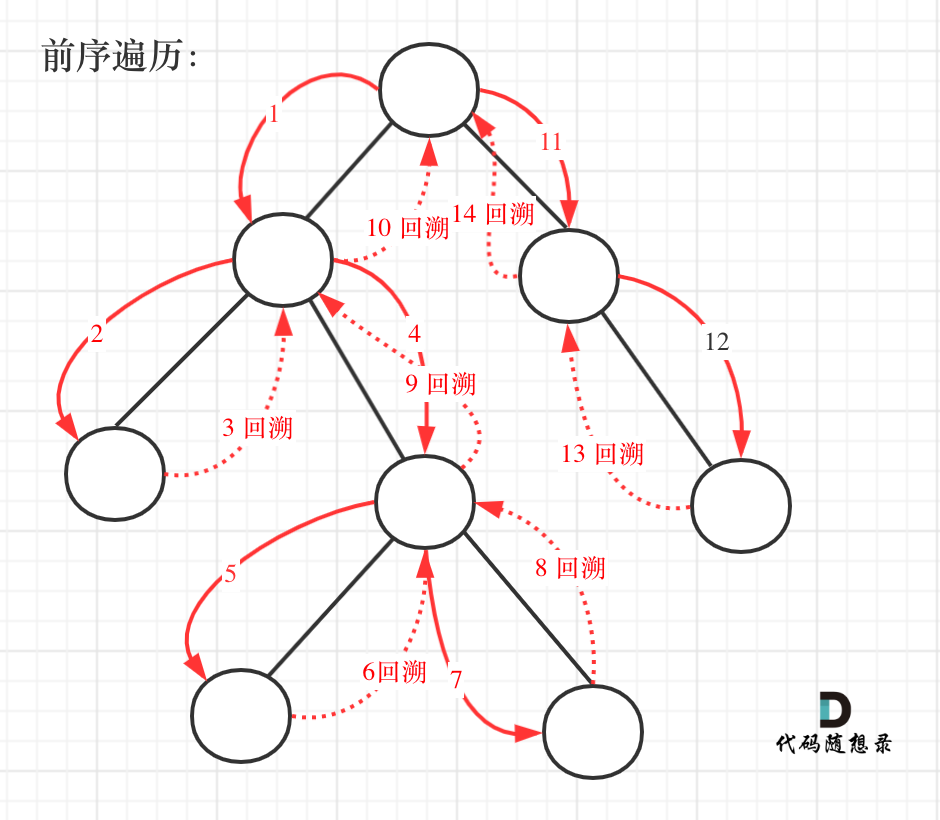
复习

深度优先遍历

前序遍历

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        preorder(root, result);
        return result;
    }

    public void preorder(TreeNode root, List<Integer> result){
        if (root == null) return;

        result.add(root.val);
        preorder(root.left, result);
        preorder(root.right, result);
    }
}

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();

        if (root == null) return result;
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            result.add(node.val);
            if (node.right != null) stack.push(node.right);
            if (node.left != null) stack.push(node.left);
        }

        return result;
    }
}

统一迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) return result;
        Stack<TreeNode> stack = new Stack<>();

        stack.push(root);

        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            if (node != null){
                if (node.right != null) stack.push(node.right);
                if (node.left != null) stack.push(node.left);

                stack.push(node);
                stack.push(null);
            } else {
                result.add(stack.pop().val);
            }
        }

        return result;
    }
}

中序遍历

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();

        inorder(root, result);

        return result;
    }
    public void inorder(TreeNode root, List<Integer> result){
        if (root == null) return;
        inorder(root.left, result);
        result.add(root.val);
        inorder(root.right, result);
    }
}

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) return result;
        Stack<TreeNode> stack = new Stack<>();

        TreeNode cur = root;

        while (cur != null || !stack.isEmpty()){
            if (cur != null){
                stack.push(cur);
                cur = cur.left;
            } else {
                cur = stack.pop();
                result.add(cur.val);
                cur = cur.right;
            }
        }

        return result;
    }
}

统一迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) return result;
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();

            if (node != null){
                if (node.right != null) stack.push(node.right);

                stack.push(node);
                stack.push(null);

                if (node.left != null) stack.push(node.left);
            } else {
                result.add(stack.pop().val);
            }
        }

        return result;
    }
}

后序遍历

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();

        postorder(root, result);

        return result;
    }

    public void postorder(TreeNode root, List<Integer> result){
        if (root == null) return;

        postorder(root.left, result);
        postorder(root.right, result);

        result.add(root.val);
    }
}

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();

        if (root == null) return result;

        Stack<TreeNode> stack = new Stack<>();

        stack.push(root);

        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            result.add(node.val);
            if (node.left != null) stack.push(node.left);
            if (node.right != null) stack.push(node.right);
        }
        Collections.reverse(result);
        
        return result;
    }
}

统一迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();

        if (root == null) return result;

        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            if (node != null){
                stack.push(node);
                stack.push(null);

                if (node.right != null) stack.push(node.right);
                if (node.left != null) stack.push(node.left);
            } else {
                result.add(stack.pop().val);
            }
        }

        return result;
    }
}

广度优先遍历

DFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> result = new ArrayList<>();

        dfs(root, 0, result);

        return result;
    }

    public void dfs(TreeNode root, int depth, List<List<Integer>> result){
        if (root == null) return;

        depth++;

        if (result.size() < depth){
            List<Integer> itemList = new ArrayList<>();
            result.add(itemList);
        }

        result.get(depth - 1).add(root.val);
        dfs(root.left, depth, result);
        dfs(root.right, depth, result);
    }
}

BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> result = new ArrayList<>();

        if (root == null) return result;

        Queue<TreeNode> queue = new ArrayDeque<>();
        queue.add(root);

        while (!queue.isEmpty()){
            List<Integer> itemList = new ArrayList<>();
            int length = queue.size();

            while (length-- > 0){
                TreeNode node = queue.poll();
                itemList.add(node.val);
                if (node.left != null) queue.add(node.left);
                if (node.right != null) queue.add(node.right); 
            }
            result.add(itemList);
        }

        return result;
    }
}

翻转二叉树

递归法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) return root;

        swapChildren(root);
        invertTree(root.left);
        invertTree(root.right);

        return root;
    }

    public void swapChildren(TreeNode root){
        TreeNode node = root.left;
        root.left = root.right;
        root.right = node;
    }
}

迭代法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) return root;

        Queue<TreeNode> queue = new ArrayDeque<>();
        queue.add(root);

        while (!queue.isEmpty()){
            TreeNode node = queue.poll();

            swapChildren(node);
            if (node.left != null) queue.add(node.left);
            if (node.right != null) queue.add(node.right);
        }

        return root;

    }

    public void swapChildren(TreeNode root){
        TreeNode node = root.left;
        root.left = root.right;
        root.right = node;
    }
}

对称二叉树

递归法

在判断左右节点的值时，不能依据两个node是否为null，那样会破坏递归，直接返回值
只能判断两个值是否相等，然后继续递归到最后

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return compare(root.left, root.right);
    }

    public boolean compare(TreeNode left, TreeNode right){
        if (left == null && right != null) return false;
        if (left != null && right == null) return false;
        if (left == null && right == null) return true;
        if (left.val != right.val) return false;

        boolean compareOutside = compare(left.left, right.right);
        boolean compareInside = compare(left.right, right.left);

        return compareOutside && compareInside;
    }
}

迭代法

建立队列时用linkedlist， ArrayDeque不接受null

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public boolean isSymmetric(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root.left);
        queue.offer(root.right);

        while (!queue.isEmpty()){
            TreeNode left = queue.poll();
            TreeNode right = queue.poll();

            if (left == null && right == null) continue;

            if (left == null || right == null || left.val != right.val) return false;

            queue.offer(left.left);
            queue.offer(right.right);
            queue.offer(left.right);
            queue.offer(right.left);
        }

        return true;
    }
}

二叉树最大深度

递归法

后序遍历

1
2
3
4
5
6
7
8
9
10
11
12

class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) return 0;
        int left = maxDepth(root.left);
        int right = maxDepth(root.right);

        int depth = 1 + Math.max(left, right);
        return depth;
    }
}

前序遍历
注意在class里面设置depth的值，进行调整，即设置环境变量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    int depth = 0;
    public int maxDepth(TreeNode root) {
        dfs(root, 0);
        return depth;
    }

    public void dfs(TreeNode root, int curDepth){
        if (root == null) return;

        curDepth++;
        depth = Math.max(curDepth, depth);
        dfs(root.left,curDepth);
        dfs(root.right,curDepth);
    }
}


层序遍历迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) return 0;

        Queue<TreeNode> queue = new ArrayDeque<>();
        queue.add(root);
        int depth = 0;
        while(!queue.isEmpty()){
            int length = queue.size();
            while (length-- > 0){
                TreeNode node = queue.poll();
                if (node.left != null) queue.add(node.left);
                if (node.right != null) queue.add(node.right);
            }
            
            depth++;
        }

        return depth;
    }
}

二叉树最小深度

后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) return 0;
        int left = minDepth(root.left);
        int right = minDepth(root.right);

        if (root.left == null){
            return 1 + right;
        }
        if (root.right == null){
            return 1 + left;
        }

        return Math.min(left, right) + 1;
        
    }
}

前序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    int depth = 0;
    int minDepth = Integer.MAX_VALUE;
    public int minDepth(TreeNode root) {
        
        getDepth(root);

        return minDepth == Integer.MAX_VALUE ? 0 : minDepth;
    }

    public void getDepth(TreeNode root){
        if (root == null) return;
        depth++;
        getDepth(root.left);
        getDepth(root.right);

        if (root.left == null && root.right== null) {
            minDepth = Math.min(minDepth, depth);
        }
        depth--;
    }

    
}

完全二叉树的节点数

后序遍历

1
2
3
4
5
6
7
8

class Solution {
    public int countNodes(TreeNode root) {
        if (root == null) return 0;
        return 1 + countNodes(root.left) + countNodes(root.right);
    }
}

前序遍历 递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

class Solution {
    int count = 0;
    public int countNodes(TreeNode root) {
        dfs(root);
        return count;
    }

    public void dfs(TreeNode root){
        if (root == null) return;
        count++;

        if (root.left != null) dfs(root.left);
        if (root.right != null) dfs(root.right);
    }

}

检查是不是满完全二叉树， 之后再返回结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution {
    public int countNodes(TreeNode root) {
        if (root == null) return 0;

        int leftDepth = 0;
        int rightDepth = 0;

        TreeNode leftNode = root.left;
        TreeNode rightNode = root.right;

        while (leftNode != null){
            leftNode = leftNode.left;
            leftDepth++;
        }

        while (rightNode != null){
            rightNode = rightNode.right;
            rightDepth++;
        }

        if (leftDepth == rightDepth){
            return (2 << leftDepth) - 1;
        }

        return 1 + countNodes(root.left) + countNodes(root.right);
    }
}

110 平衡二叉树

https://leetcode.com/problems/balanced-binary-tree/

判断一个二叉树每个节点左右两个子树的高度差绝对值不超过一

求高度 用后序遍历
求深度 用前序遍历

在用后序遍历时 求左子树和右子树的高度差值，如果差值小于等于1，返回当前二叉树高度，否则-1；
返回当前节点为根节点的树的最大高度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution {
    public boolean isBalanced(TreeNode root) {
        return getHeight(root) != -1;
    }

    public int getHeight(TreeNode root){
        if (root == null) return 0;

        int leftHeight = getHeight(root.left);
        if (leftHeight == -1) return -1;
        int rightHeight = getHeight(root.right);
        if (rightHeight == -1) return -1;
        if (Math.abs(leftHeight - rightHeight) > 1){
            return -1;
        }

        return Math.max(leftHeight, rightHeight) + 1;
    }
}


257 二叉树的所有路径

https://leetcode.com/problems/binary-tree-paths/description/

返回从根节点到叶子节点所有路径 需要前序遍历

此题难点是回溯
在前序遍历之中，进行回溯
在前序遍历添加到result数组之后返回

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> result = new ArrayList<>();

        if (root == null) return result;

        List<Integer> paths = new ArrayList<>();

        traversal(root, result, paths);

        return result;
    }

    public void traversal(TreeNode root, List<String> result, List<Integer> paths){
        paths.add(root.val);
        if (root.left == null && root.right == null){
            StringBuilder sb = new StringBuilder();
            
            for (int i = 0; i < paths.size() - 1; i++){
                sb.append(paths.get(i)).append("->");
            }
            sb.append(paths.get(paths.size() - 1));
            result.add(sb.toString());
        }

        if (root.left != null){
            traversal(root.left, result, paths);
            paths.remove(paths.get(paths.size() - 1));
        }

        if (root.right != null){
            traversal(root.right, result, paths);
            paths.remove(paths.get(paths.size() - 1));
        }
    }
}

迭代法
把路径和node一起推入栈中，node节点为叶子结点时，添加result，否则，就把下一个path写进stack中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> result = new ArrayList<>();
        if (root == null) return result;

        Stack<Object> stack = new Stack<>();
        stack.push(root);
        stack.push(root.val + "");

        while (!stack.isEmpty()){
            String path = (String) stack.pop();
            TreeNode node = (TreeNode) stack.pop();

            if (node.left == null && node.right == null){
                result.add(path);
            }

            if (node.right != null) {
                stack.push(node.right);
                stack.push(path + "->" + node.right.val);
            }

            if (node.left != null){
                stack.push(node.left);
                stack.push(path + "->" + node.left.val);
            }
        }

        return result;
    }
}

404 左叶子之和

计算给定二叉树的所有左叶子之和
判断左叶子的方法，就是该节点的左节点不为空，该节点的左节点的左节点和左节点的右节点为空，则该节点的左节点为左叶子结点

递归法 通过后序遍历完成

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) return 0;
        if (root.left == null && root.right == null) return 0;
        int leftSum = sumOfLeftLeaves(root.left);
        int rightSum = sumOfLeftLeaves(root.right);

        int midValue = 0;

        if (root.left != null && root.left.left == null && root.left.right == null){
            midValue = root.left.val;
        }

        return leftSum + rightSum + midValue;
    }
}

迭代法

一个前序迭代，就可以完成

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();

        if (root != null) stack.push(root);
        if (root == null) return 0;
        int sum = 0;
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            if (node.left != null && node.left.left == null && node.left.right == null){
                sum += node.left.val;
            }
            if (node.right != null) stack.push(node.right);
            if (node.left != null) stack.push(node.left);
        }

        return sum;

    }
}