复习 深度优先遍历 递归
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution { List<Integer> result = new ArrayList <>(); public List<Integer> inorderTraversal (TreeNode root) { if (root == null ) return result; inorder(root); return result; } private void inorder (TreeNode node) { if (node == null ) return ; inorder(node.left); result.add(node.val); inorder(node.right); } }
迭代
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution { public List<Integer> preorderTraversal (TreeNode root) { List<Integer> result = new ArrayList <>(); if (root == null ) return result; Stack<TreeNode> stack = new Stack <>(); stack.push(root); while (!stack.isEmpty()){ TreeNode node = stack.pop(); result.add(node.val); if (node.right != null ) stack.push(node.right); if (node.left != null ) stack.push(node.left); } return result; } }
中序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution { public List<Integer> inorderTraversal (TreeNode root) { List<Integer> result = new ArrayList <>(); if (root == null ) return result; Stack<TreeNode> stack = new Stack <>(); TreeNode cur = root; while (cur != null || !stack.isEmpty()){ if (cur != null ){ stack.push(cur); cur = cur.left; } else { cur = stack.pop(); result.add(cur.val); cur = cur.right; } } return result; } }
后序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution { public List<Integer> postorderTraversal (TreeNode root) { List<Integer> result = new ArrayList <>(); if (root == null ) return result; Stack<TreeNode> stack = new Stack <>(); stack.push(root); while (!stack.isEmpty()){ TreeNode node = stack.pop(); result.add(node.val); if (node.left != null ) stack.push(node.left); if (node.right != null ) stack.push(node.right); } Collections.reverse(result); return result; } }
统一迭代
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution { public List<Integer> inorderTraversal (TreeNode root) { List<Integer> result = new ArrayList <>(); if (root == null ) return result; Stack<TreeNode> stack = new Stack <>(); stack.push(root); while (!stack.isEmpty()){ TreeNode node = stack.pop(); if (node != null ){ if (node.right != null ) stack.push(node.right); stack.push(node); stack.push(null ); if (node.left != null ) stack.push(node.left); } else { result.add(stack.pop().val); } } return result; } }
DFS
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution { List<List<Integer>> result = new ArrayList <>(); public List<List<Integer>> levelOrder (TreeNode root) { if (root == null ) return result; dfs(root, 0 ); return result; } private void dfs (TreeNode node, int depth) { if (node == null ) return ; depth++; if (depth > result.size()){ result.add(new ArrayList <Integer>()); } result.get(depth - 1 ).add(node.val); if (node.left != null ) dfs(node.left, depth); if (node.right != null ) dfs(node.right, depth); } }
广度优先遍历 BFS
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution { public List<List<Integer>> levelOrder (TreeNode root) { List<List<Integer>> result = new ArrayList <>(); if (root == null ) return result; Queue<TreeNode> queue = new LinkedList <>(); queue.offer(root); while (!queue.isEmpty()){ int length = queue.size(); List<Integer> itemList = new ArrayList <>(); while (length-- > 0 ){ TreeNode node = queue.poll(); itemList.add(node.val); if (node.left != null ) queue.offer(node.left); if (node.right != null ) queue.offer(node.right); } result.add(itemList); } return result; } }
226 翻转二叉树 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution { public TreeNode invertTree (TreeNode root) { if (root == null ) return root; swapChildren(root); invertTree(root.left); invertTree(root.right); return root; } private void swapChildren (TreeNode node) { TreeNode temp = node.left; node.left = node.right; node.right = temp; } }
101 对称二叉树 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution { public boolean isSymmetric (TreeNode root) { if (root == null ) return true ; return compare(root.left, root.right); } private boolean compare (TreeNode left, TreeNode right) { if (left == null && right == null ) return true ; if (left == null || right == null || left.val != right.val) return false ; boolean compareOutside = compare(left.left, right.right); boolean compareInside = compare(left.right, right.left); return compareInside && compareOutside; } }
104 二叉树最大深度 1 2 3 4 5 6 7 class Solution { public int maxDepth (TreeNode root) { if (root == null ) return 0 ; return 1 + Math.max(maxDepth(root.left), maxDepth(root.right)); } }
111 二叉树最小深度 递归
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution { int mindepth = Integer.MAX_VALUE; public int minDepth (TreeNode root) { if (root == null ) return 0 ; dfs(root,0 ); return mindepth; } private void dfs (TreeNode root, int depth) { if (root == null ) return ; depth++; if (root.left == null && root.right == null ){ if (mindepth > depth){ mindepth = Math.min(depth, mindepth); return ; } } if (root.left != null ){ dfs(root.left, depth); } if (root.right != null ){ dfs(root.right, depth); } } }
迭代
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution { public int minDepth (TreeNode root) { if (root == null ) return 0 ; Queue<TreeNode> queue = new LinkedList <>(); queue.offer(root); int depth = 0 ; while (!queue.isEmpty()){ int length = queue.size(); depth++; while (length-- > 0 ){ TreeNode node = queue.poll(); if (node.left == null && node.right == null ){ return depth; } if (node.left != null ) queue.offer(node.left); if (node.right != null ) queue.offer(node.right); } } return depth; } }
222 完全二叉树节点个数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution { public int countNodes (TreeNode root) { if (root == null ) return 0 ; TreeNode left = root.left; TreeNode right = root.right; int leftDepth = 0 ; int rightDepth = 0 ; while (left != null ){ left = left.left; leftDepth++; } while (right != null ){ right = right.right; rightDepth++; } if (leftDepth == rightDepth){ return (2 << leftDepth) - 1 ; } return 1 + countNodes(root.left) + countNodes(root.right); } }
110 平衡二叉树 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution { public boolean isBalanced (TreeNode root) { return getHeight(root) != -1 ; } private int getHeight (TreeNode root) { if (root == null ) return 0 ; int left = getHeight(root.left); if (left == -1 ) return -1 ; int right = getHeight(root.right); if (right == -1 ) return -1 ; if (Math.abs(left - right) > 1 ){ return -1 ; } return 1 + Math.max(left, right); } }
257 二叉树的所有路径 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution { List<String> result = new ArrayList <>(); public List<String> binaryTreePaths (TreeNode root) { if (root == null ) return result; List<Integer> paths = new ArrayList <>(); getPaths(root, paths); return result; } private void getPaths (TreeNode root, List<Integer> paths) { paths.add(root.val); if (root.left == null && root.right == null ){ StringBuilder sb = new StringBuilder (); for (int i = 0 ; i < paths.size() - 1 ; i++){ sb.append(paths.get(i)).append("->" ); } sb.append(paths.get(paths.size() - 1 )); result.add(sb.toString()); return ; } if (root.left != null ) { getPaths(root.left, paths); paths.remove(paths.size() - 1 ); } if (root.right != null ) { getPaths(root.right, paths); paths.remove(paths.size() - 1 ); } } }
404 左叶子之和 1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution { int sum = 0 ; public int sumOfLeftLeaves (TreeNode root) { if (root == null ) return 0 ; if (root.left != null && root.left.left == null && root.left.right == null ){ sum += root.left.val; } if (root.left != null ) sumOfLeftLeaves(root.left); if (root.right != null ) sumOfLeftLeaves(root.right); return sum; } }
513 找树左下角的值 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution { public int findBottomLeftValue (TreeNode root) { if (root == null ) return 0 ; Queue<TreeNode> queue = new LinkedList <>(); queue.offer(root); int result = 0 ; while (!queue.isEmpty()){ int length = queue.size(); for (int i = 0 ; i < length; i++){ TreeNode node = queue.poll(); if (i == 0 ){ result = node.val; } if (node.left != null ) queue.offer(node.left); if (node.right != null ) queue.offer(node.right); } } return result; } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution { int val = 0 ; int maxDepth = 0 ; public int findBottomLeftValue (TreeNode root) { if (root == null ) return val; dfs(root, 0 ); return val; } private void dfs (TreeNode root, int depth) { depth++; if (root.left == null && root.right == null ){ if (depth > maxDepth){ maxDepth = depth; val = root.val; } } if (root.left != null ) dfs(root.left, depth); if (root.right != null ) dfs(root.right, depth); } }
112 路径总和 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution { public boolean hasPathSum (TreeNode root, int targetSum) { if (root == null ) return false ; targetSum -= root.val; if (root.left == null && root.right == null ){ if (targetSum == 0 ){ return true ; } } boolean left = hasPathSum(root.left, targetSum); boolean right = hasPathSum(root.right,targetSum); return left || right; } }
113 路径总和II 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution { List<List<Integer>> result = new ArrayList <>(); public List<List<Integer>> pathSum (TreeNode root, int targetSum) { if (root == null ) return result; List<Integer> paths = new ArrayList <>(); getPaths(root, paths, targetSum); return result; } private void getPaths (TreeNode node, List<Integer> paths, int targetSum) { paths.add(node.val); targetSum -= node.val; if (node.left == null && node.right == null ){ if (targetSum == 0 ){ result.add(new ArrayList <Integer>(paths)); } } if (node.left != null ){ getPaths(node.left, paths, targetSum); paths.remove(paths.size() - 1 ); } if (node.right != null ){ getPaths(node.right, paths, targetSum); paths.remove(paths.size() - 1 ); } } }
106 从中序与后序遍历序列构造二叉树 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution { Map<Integer, Integer> map = new HashMap <>(); public TreeNode buildTree (int [] inorder, int [] postorder) { if (inorder.length == 0 ) return null ; for (int i = 0 ; i < inorder.length; i++){ map.put(inorder[i], i); } return buildHelper(inorder, 0 , inorder.length, postorder, 0 , postorder.length); } private TreeNode buildHelper (int [] inorder, int inS, int inE, int [] postorder, int postS, int postE) { if (inS >= inE || postS >= postE) return null ; int rootVal = postorder[postE - 1 ]; int rootIndex = map.get(rootVal); int lengthOfLeft = rootIndex - inS; TreeNode root = new TreeNode (rootVal); root.left = buildHelper(inorder, inS, rootIndex, postorder, postS, postS + lengthOfLeft); root.right = buildHelper(inorder, rootIndex + 1 , inE, postorder, postS + lengthOfLeft, postE - 1 ); return root; } }
105 从前序与中序遍历序列构造二叉树 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution { Map<Integer, Integer> map = new HashMap <>(); public TreeNode buildTree (int [] preorder, int [] inorder) { if (preorder.length == 0 ) return null ; for (int i = 0 ; i < inorder.length; i++){ map.put(inorder[i], i); } return buildHelper(preorder, 0 , preorder.length, inorder, 0 , inorder.length); } private TreeNode buildHelper (int [] preorder, int preS, int preE, int [] inorder, int inS, int inE) { if (preS >= preE || inS >= inE) return null ; int rootVal = preorder[preS]; int rootIndex = map.get(rootVal); int lenOfLeft = rootIndex - inS; TreeNode root = new TreeNode (rootVal); root.left = buildHelper(preorder, preS + 1 , preS + lenOfLeft + 1 , inorder, inS, rootIndex); root.right = buildHelper(preorder, preS + lenOfLeft + 1 , preE, inorder, rootIndex + 1 , inE); return root; } }
654 最大二叉树 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution { public TreeNode constructMaximumBinaryTree (int [] nums) { if (nums.length == 0 ) return null ; return constructHelper(nums, 0 , nums.length); } private TreeNode constructHelper (int [] nums, int start, int end) { if (start >= end) return null ; int [] max = getMaximum(nums, start, end); int maxValue = max[0 ]; int maxIndex = max[1 ]; TreeNode root = new TreeNode (maxValue); root.left = constructHelper(nums, start, maxIndex); root.right = constructHelper(nums, maxIndex + 1 , end); return root; } private int [] getMaximum(int [] nums, int start, int end){ int maxVal = Integer.MIN_VALUE; int index = start; for (int i = start; i < end; i++){ if (nums[i] > maxVal){ maxVal = nums[i]; index = i; } } return new int [] {maxVal, index}; } }
617 合并二叉树 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution { public TreeNode mergeTrees (TreeNode root1, TreeNode root2) { if (root1 == null && root2 == null ) return null ; if (root1 == null && root2 != null ) return root2; if (root1 != null && root2 == null ) return root1; TreeNode root = new TreeNode (root1.val + root2.val); root.left = mergeTrees(root1.left, root2.left); root.right = mergeTrees(root1.right, root2.right); return root; } }
700 二叉搜索树中的搜索 1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution { public TreeNode searchBST (TreeNode root, int val) { if (root == null ) return null ; if (root.val == val){ return root; } else if (root.val > val){ return searchBST(root.left, val); } else { return searchBST(root.right, val); } } }
98 验证二叉搜索树 中序递归判断数组
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution { List<Integer> result = new ArrayList <>(); public boolean isValidBST (TreeNode root) { if (root == null ) return true ; inorder(root); return isInOrder(result); } private void inorder (TreeNode root) { if (root == null ) return ; inorder(root.left); result.add(root.val); inorder(root.right); } private boolean isInOrder (List<Integer> result) { for (int i = 1 ; i < result.size(); i++){ if (result.get(i - 1 ) >= result.get(i)) return false ; } return true ; } }
记录上一个node 比较root和node的大小
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution { TreeNode max; public boolean isValidBST (TreeNode root) { if (root == null ) return true ; boolean left = isValidBST(root.left); if (!left) return false ; if (max != null && root.val <= max.val) return false ; max = root; boolean right = isValidBST(root.right); return right; } }
107 二叉树的层次遍历II 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution { List<List<Integer>> result = new ArrayList <>(); public List<List<Integer>> levelOrderBottom (TreeNode root) { if (root == null ) return result; Queue<TreeNode> queue = new LinkedList <>(); queue.offer(root); while (!queue.isEmpty()){ int length = queue.size(); List<Integer> item = new ArrayList <>(); while (length-- > 0 ){ TreeNode node = queue.poll(); item.add(node.val); if (node.left != null ) queue.offer(node.left); if (node.right != null ) queue.offer(node.right); } result.add(item); } Collections.reverse(result); return result; } }
199 二叉树的右视图 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution { List<Integer> result = new ArrayList <>(); public List<Integer> rightSideView (TreeNode root) { if (root == null ) return result; Queue<TreeNode> queue = new LinkedList <>(); queue.offer(root); while (!queue.isEmpty()){ int length = queue.size(); while (length-- > 0 ){ TreeNode node = queue.poll(); if (length == 0 ){ result.add(node.val); } if (node.left != null ) queue.offer(node.left); if (node.right != null ) queue.offer(node.right); } } return result; } }
530 二叉搜索树的最小绝对差 利用中序遍历二叉搜索树,比较当前值和之前的值的差值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution { List<Integer> result = new ArrayList <>(); public int getMinimumDifference (TreeNode root) { if (root == null ) return 0 ; inorder(root); int min = Integer.MAX_VALUE; for (int i = 1 ; i < result.size(); i++){ int diff = result.get(i) - result.get(i -1 ); if (diff < min) { min = diff; } } return min; } private void inorder (TreeNode node) { if (node == null ) return ; inorder(node.left); result.add(node.val); inorder(node.right); } }
在中序遍历之中记录一个pre node 之后再记录min的差值,进行比较,二叉搜索树特性
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution { int min = Integer.MAX_VALUE; TreeNode pre; public int getMinimumDifference (TreeNode root) { if (root == null ) return 0 ; getMinimumDifference(root.left); if (pre != null && Math.abs(pre.val - root.val) < min) min = Math.abs(pre.val - root.val); pre = root; getMinimumDifference(root.right); return min; } }
501 二叉搜索树中的众数 利用map 前序遍历计数,然后再统计出现频率最多的数字
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution { Map<Integer, Integer> map = new HashMap <>(); List<Integer> result = new ArrayList <>(); public int [] findMode(TreeNode root) { preorder(root); List<Map.Entry<Integer, Integer>> mapList = map.entrySet().stream() .sorted((c1, c2) -> c2.getValue().compareTo(c1.getValue())) .collect(Collectors.toList()); result.add(mapList.get(0 ).getKey()); for (int i = 1 ; i < mapList.size(); i++) { if (mapList.get(i).getValue() == mapList.get(i - 1 ).getValue()) { result.add(mapList.get(i).getKey()); } else { break ; } } return result.stream().mapToInt(Integer::intValue).toArray(); } private void preorder (TreeNode root) { if (root == null ) return ; if (map.containsKey(root.val)){ map.put(root.val, map.get(root.val) + 1 ); } else { map.put(root.val, 1 ); } preorder(root.left); preorder(root.right); } }
一次中序遍历利用二叉搜索树特性
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 class Solution { List<Integer> result = new ArrayList <>(); int maxCount = 0 ; int count = 0 ; TreeNode pre; public int [] findMode(TreeNode root) { inorder(root); int [] res = new int [result.size()]; for (int i = 0 ; i < result.size(); i++) { res[i] = result.get(i); } return res; } private void inorder (TreeNode root) { if (root == null ) return ; inorder(root.left); if (pre == null ){ count = 1 ; } else if (pre.val == root.val){ count++; } else { count = 1 ; } pre = root; if (count > maxCount){ result.clear(); result.add(root.val); maxCount = count; } else if (count == maxCount){ result.add(root.val); } inorder(root.right); } }
迭代法同理,在处理node时同样的逻辑
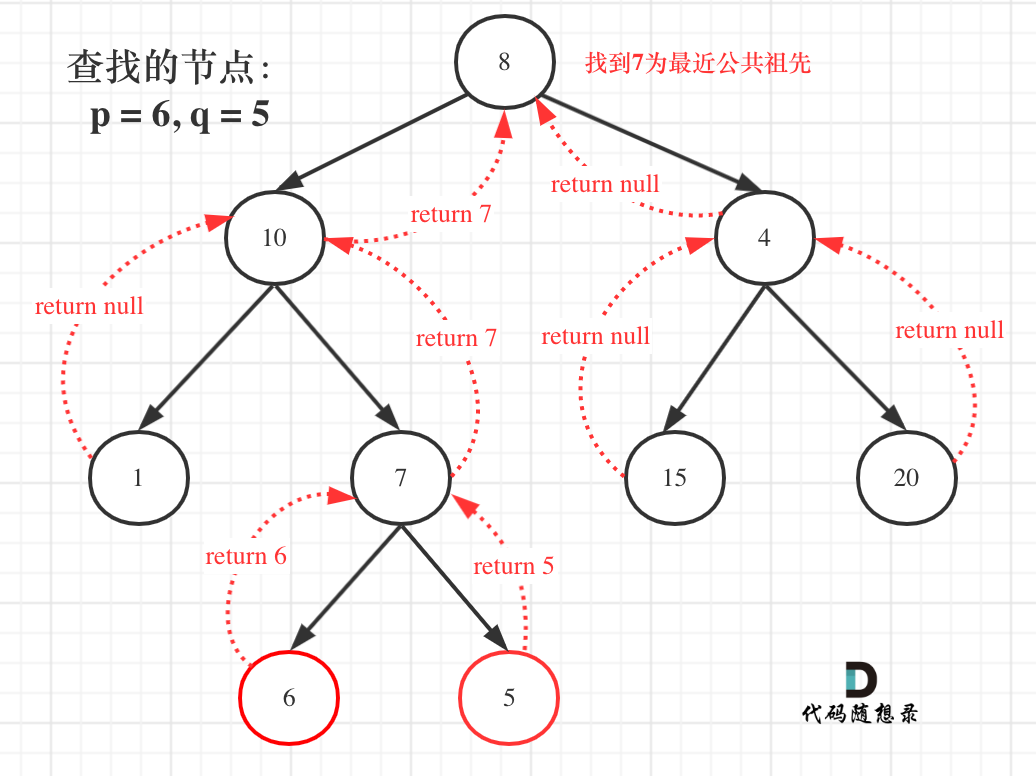
236 二叉树的最近公共祖先 此题是自底向上查找,就是回溯
如果有一个节点,发现左子树出现节点P,右子树出现节点q,或者相反,那么该节点就是公共祖先
如果遇到p 返回p如果遇到q返回q,如果左右子树不为空,中节点就是最近祖先
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution { public TreeNode lowestCommonAncestor (TreeNode root, TreeNode p, TreeNode q) { if (root == null || root == p || root == q){ return root; } TreeNode left = lowestCommonAncestor(root.left, p, q); TreeNode right = lowestCommonAncestor(root.right, p , q); if (left != null && right != null ) return root; if (left == null && right != null ) return right; else if (left != null && right == null ) return left; else return null ; } }