代码随想录第二十四天

Posted on In

回溯算法理论基础

回溯法也叫回溯搜索法是一种搜索方式

只要有递归就有回溯
回溯的本质是穷举，穷举所有可能，选出想要的答案，使他变高效可以剪枝

回溯可以解决的问题

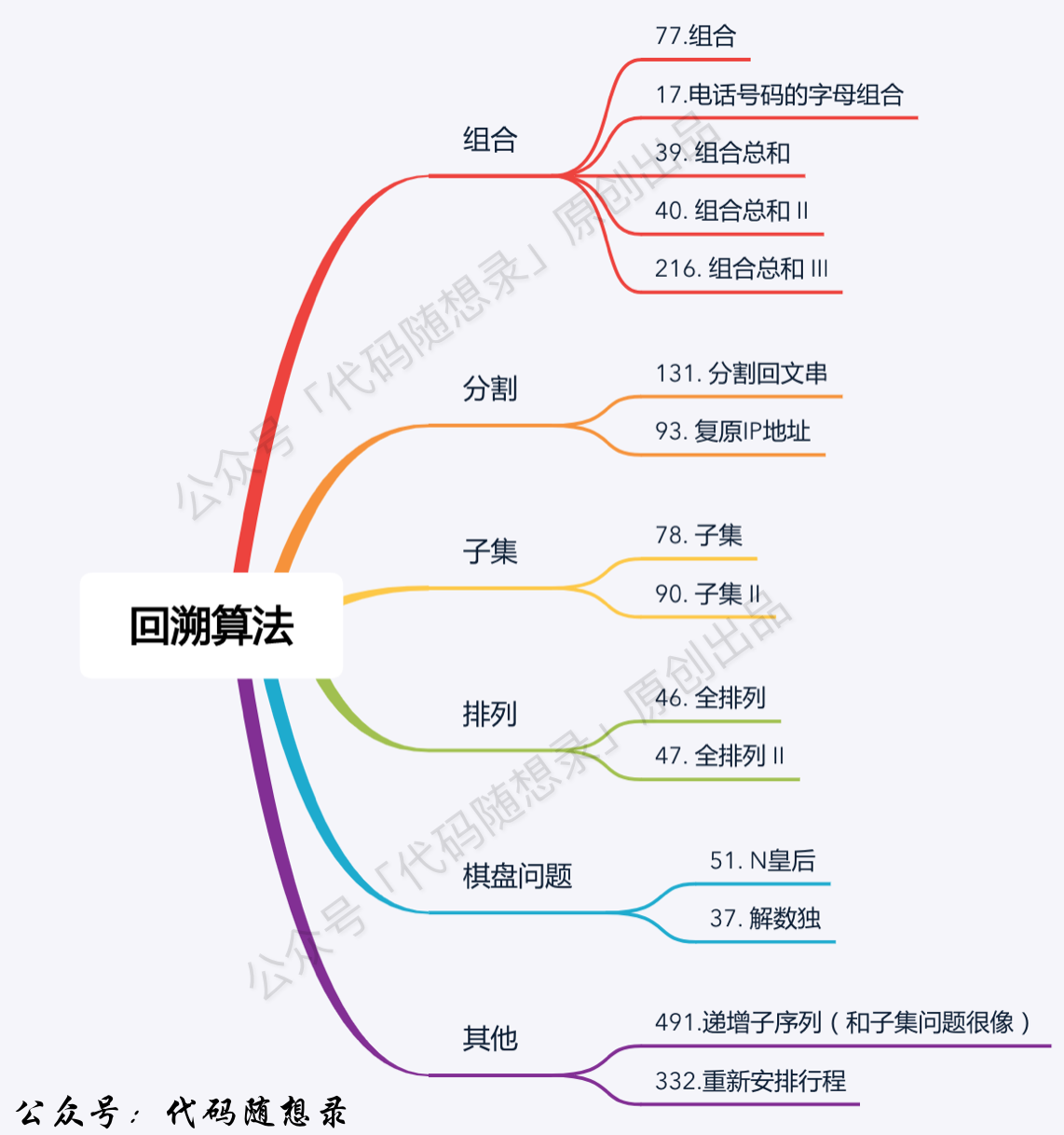
组合问题：N个数里面按一定规则找出K个数的集合
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合有多少符合条件的集合
排列问题：N个数按一定规则排列，有几种排列方式
棋盘问题：N皇后，解数独

组合是不强调顺序的，排列是强调顺序的

理解回溯

回溯解决的问题都可以抽象成树形结构

解决的都是在集合中递归查找子集，集合的大小就构成树的宽度，递归的深度就是树的深度

递归有终止条件，必然是一颗高度有限的树（N叉树）

回溯法模版

对应递归三部曲

回溯函数模版返回值以及参数

函数起名：backtracking
函数返回：void

参数不确定，一般是需要什么参数，再后填参数

伪代码为

1
private void backtracking(参数)

回溯函数终止条件

对应遍历树形结构需要终止条件
在回溯中，一般遍历到叶子结点，即满足条件，保存结果并返回

伪代码为

1
2
3
4
if (终止条件){
	保存结果;
	return;
}

回溯搜索的遍历过程

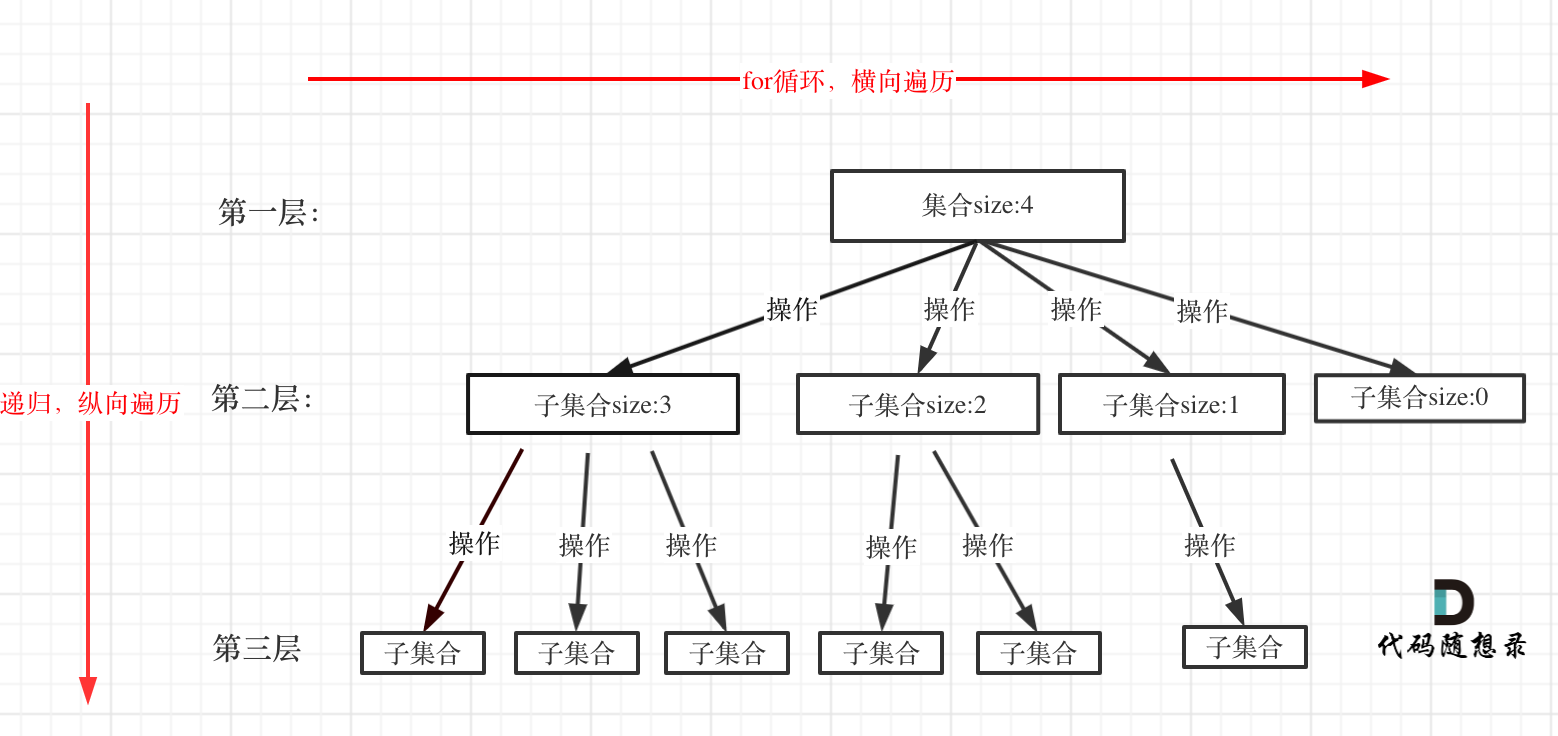
利用for循环进行横向遍历，利用递归进行纵向遍历

伪代码为

1
2
3
4
5
6
7
8
for (选择： 本层集合中的元素（树中节点孩子的数量就是集合的大小）){

	处理节点
	backTracking(路径，选择列表)；//递归
	回溯,撤销处理结果
}


77 组合

给定n, k，找出所有【1，n】集合中k个数的组合

利用回溯模版

首先确定result 和 path数组
利用path进行回溯

模拟回溯过程，见图

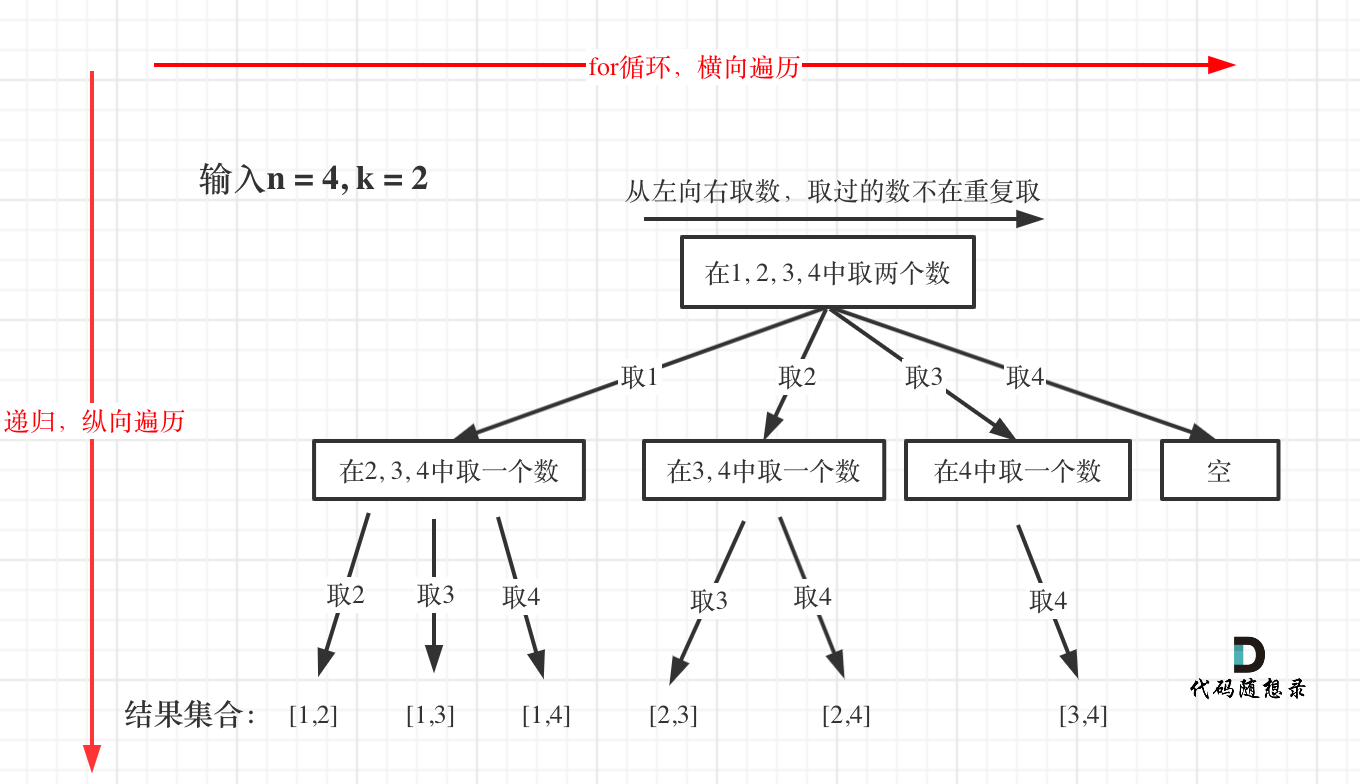
需要一个startIndex确定

以 n = 4，k = 2为例
回溯的终止条件，是path里面有两个值

利用for loop 遍历 1234， 在遍历过程中嵌套一个递归函数，就会有第二个for loop，此时第二个for loop 需要从i + 1开始
所以回溯此时就是多嵌套几次for loop

具体实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    public List<List<Integer>> combine(int n, int k) {
        backtracking(n, k, 1);
        return result;
    }

    private void backtracking(int n, int k, int start){
        if (path.size() == k){
            result.add(new ArrayList<>(path));
            return;
        }

        for (int i = start; i <= n; i++){
            path.add(i);
            backtracking(n,k,i+1);
            path.remove(path.size() - 1);
        }
    }
}

在此基础上进行剪枝操作，优化当前逻辑
以n = 4 k = 4举例

在1234中选择后
下一层只可能从234中选择，34,4都是可以减掉的
同理再下一层只可能从34中选择，4可以减掉

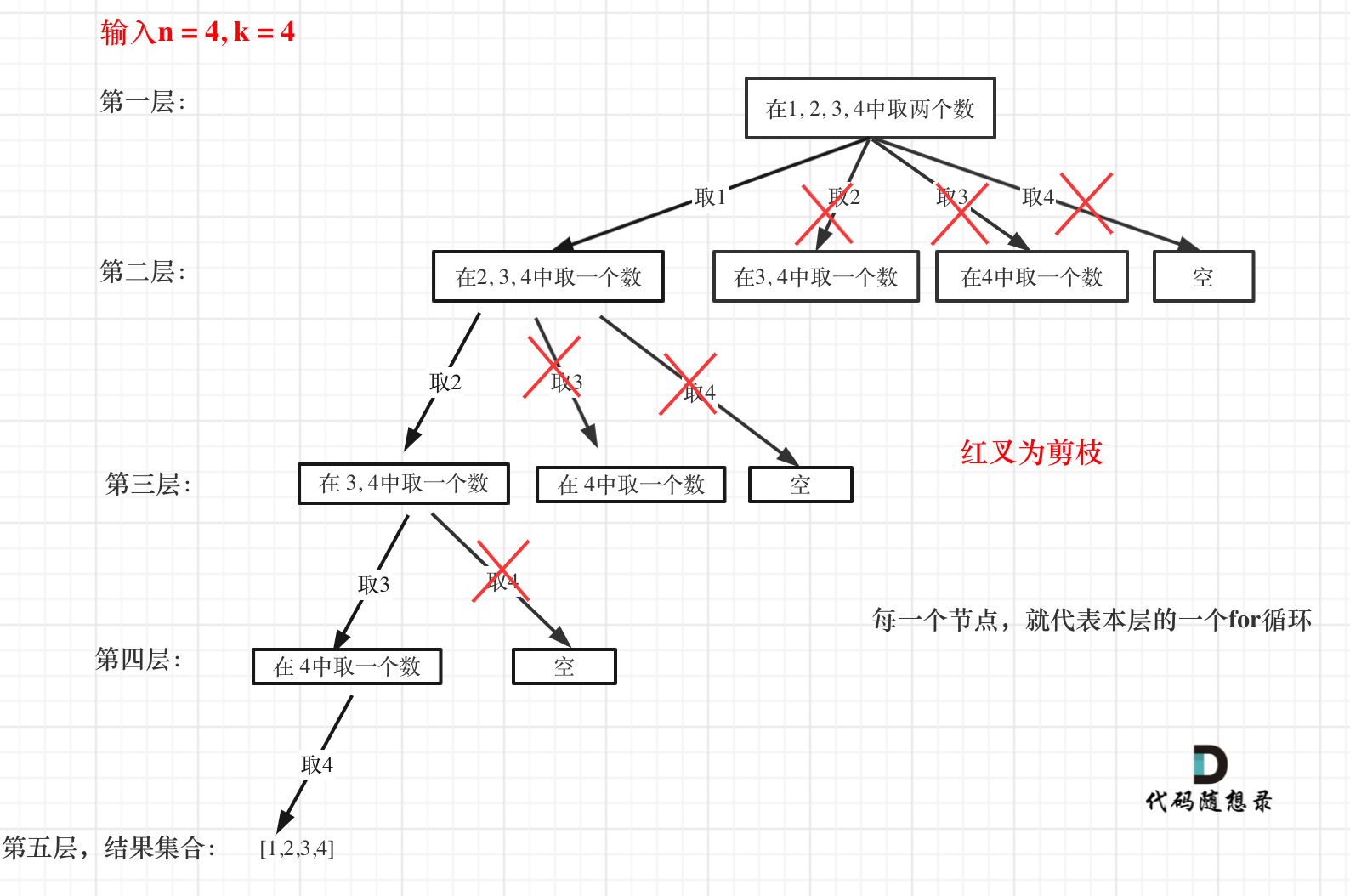
剪枝部分就是每一层中for loop 所选择的起始位置

for loop中不需要遍历到n 需要调整i遍历到哪里停止

思考逻辑：
已经选取的元素个数是path.size()
所以所需元素个数为 k - path.size()
所以此时i的最大值为 n - (k - path.size()) + 1，之后的都可以不用遍历

具体代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    public List<List<Integer>> combine(int n, int k) {
        backtracking(n, k, 1);

        return result;
    }

    private void backtracking(int n, int k, int start){
        if (path.size() == k){
            result.add(new ArrayList<>(path));
            return;
        }

        for (int i = start; i <= n - k + path.size() + 1; i++){
            path.add(i);
            backtracking(n, k, i + 1);
            path.remove(path.size() - 1);
        }
    }
}

将回溯过程抽象成树结构进行思考