代码随想录第二十七天

Posted on Edited on In

复习

回溯结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17


private void backtracking(...){
if (终止条件){
	保存结果;
	return;
}
	
for (选择： 本层集合中的元素（树中节点孩子的数量就是集合的大小）){

	处理节点
	backTracking(路径，选择列表)；//递归
	回溯,撤销处理结果
}

}

77 组合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    public List<List<Integer>> combine(int n, int k) {
        getPath(n, k, 1);

        return result;
    }

    private void getPath(int n, int k, int start){
        if (path.size() == k){
            result.add(new ArrayList<>(path));
            return;
        }

        for (int i = start; i <= n - (k - path.size()) + 1; i++){
            path.add(i);
            getPath(n, k, i + 1);
            path.remove(path.size() - 1);
        }
    }
}

216 组合总和III

判断n时，如果n< 0 则直接返回
还有for loop 中的判断条件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
        backTracking(k, n, 1);
        return result;
    }

    private void backTracking(int k, int n, int start){
        if (n < 0) return;
        if (n == 0 && path.size() == k){
            result.add(new ArrayList<>(path));
            return;
        }

        for (int i = start; i <= 9 - (k - path.size()) + 1; i++){
            path.add(i);
            n -= i;
            backTracking(k, n, i + 1);
            n += i;
            path.remove(path.size() - 1);
        }
    }
}

17 电话号码的字母组合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
    List<String> result = new ArrayList<>();
    StringBuilder sb = new StringBuilder();
    public List<String> letterCombinations(String digits) {
        if (digits == null || digits.length() == 0) return result;
        backTracking(digits, 0);
        return result;
    }

    private void backTracking(String digits, int index){
        if (sb.length() == digits.length()){
            result.add(sb.toString());
            return;
        }

        String str = numString[digits.charAt(index) - '0'];
        for (int i = 0; i < str.length(); i++){
            sb.append(str.charAt(i));
            backTracking(digits, index + 1);
            sb.deleteCharAt(sb.length() - 1);
        }
        
    }
}

39 组合总和

本体没有数量要求，可以无限重复，但总和有限制，需要的就是解决答案重复问题

此时利用start， 将函数锁定，只能向后或当前元素选取即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
    List<List<Integer>> result = new ArrayList<>();

    List<Integer> path = new ArrayList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        backTracking(candidates, target, 0);
        return result;
    }

    private void backTracking(int[] candidates, int target, int start){
        if (target < 0) return;
        if (target == 0){
            result.add(new ArrayList<>(path));
        }

        for (int i = start; i < candidates.length; i++){
            path.add(candidates[i]);
            target -= candidates[i];
            backTracking(candidates, target, i);
            target += candidates[i];
            path.remove(path.size() - 1);
        }
    }
}

剪枝优化
把candidates sort一下，这样可以减少操作，可以把对n的判断放到循环内部减少时间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        backTracking(candidates, target, 0);
        return result;
    }

    private void backTracking(int[] candidates, int target, int start){
        if (target == 0){
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = start; i < candidates.length; i++){
            if (target < 0) break;
            target -= candidates[i];
            path.add(candidates[i]);
            backTracking(candidates, target, i);
            target += candidates[i];
            path.remove(path.size() - 1);

        }
    }
}

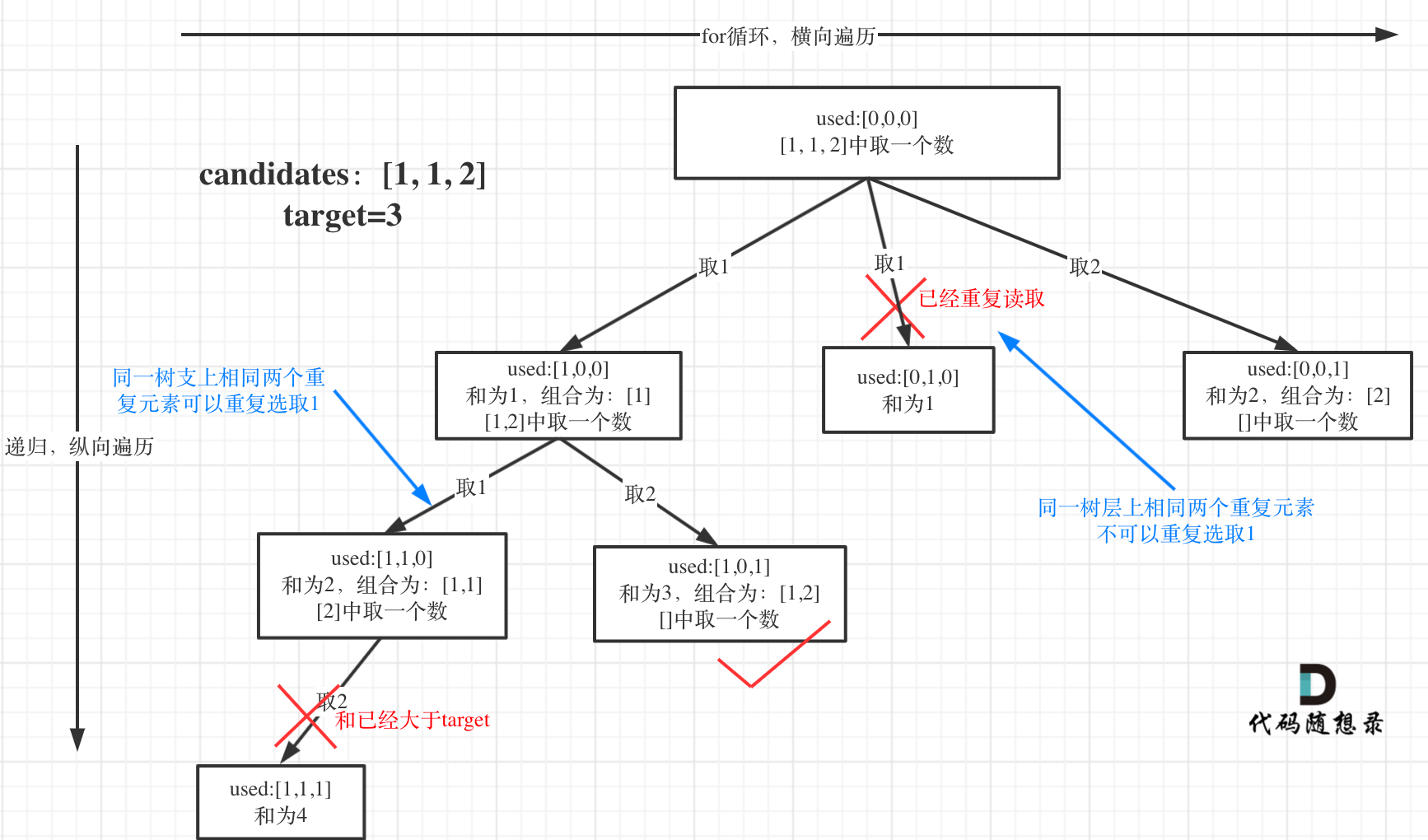
40 组合总和II

组合问题的去重

难点在于candidates里面有重复元素但是不能有重复组合

从树的结构上，同一个树层上不能重复选取相同的值，这样会重复读取

在同一层上要记录选取过的元素

基本结构不变，利用used boolean数组

首先sort candidates数组 记录used数组全部false

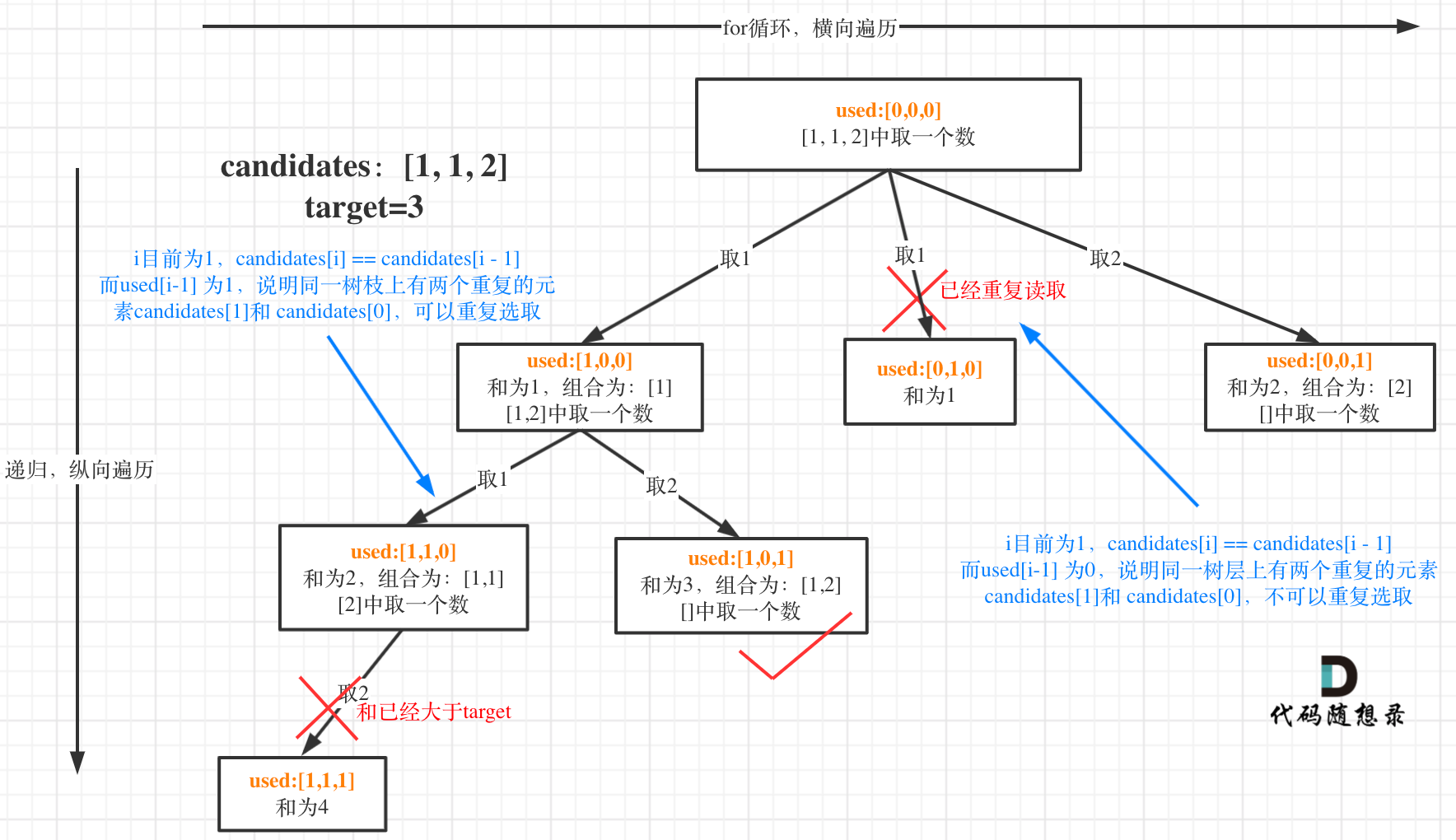
比较candidates的这一位和前一位是不是同一个数，如果是，如果前一位已经被用了，就跳过此次循环

如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false，就说明：前一个树枝，使用了candidates[i - 1]，也就是说同一树层使用过candidates[i - 1]。
used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
used[i - 1] == false，说明同一树层candidates[i - 1]使用过

添加 回溯used数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
 class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    boolean[] used;
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        used = new boolean[candidates.length];
        Arrays.fill(used, false);
        if (candidates == null || candidates.length == 0) return result;
        Arrays.sort(candidates);
        backTracking(candidates, target, 0);
        return result;
    }

    private void backTracking(int[] candidates, int target, int start){
        if (target == 0){
            result.add(new ArrayList<>(path));
            return;
        }

        for (int i = start; i < candidates.length; i++){
            if (target < 0) break;
            if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) continue; 
            used[i] = true;
            target -= candidates[i];
            path.add(candidates[i]);
            backTracking(candidates, target, i + 1);
            used[i] = false;
            path.remove(path.size() - 1);
            target += candidates[i];
        }

    }
}

131 分割回文串

此题为分割问题

第一要分割，第二要判断回文

每段依次分割
需要切割线 startIndex
还需要判断回文函数

具体实现
利用分割点，判断该子字符串是否为回文，是的话，回溯函数，不是就是continue

string的子字符串取法：
s.substring(string, start, end);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    List<List<String>> result = new ArrayList<>();
    List<String> path = new ArrayList<>();
    public List<List<String>> partition(String s) {
        backTracking(s, 0);
        return result;
    }

    private void backTracking(String s, int start){
        if (start == s.length()){
            result.add(new ArrayList(path));
            return;
        }
        for(int i = start; i < s.length(); ++i) {
            if(isPalindrome(s, start, i)) {
                path.add(s.substring(start, i+1));
                backTracking(s, i+1);
                path.remove(path.size()-1);
            }
        }
    }
    private boolean isPalindrome(String s, int left, int right){
        while (left <= right){
            if (s.charAt(left) == s.charAt(right)){
                left++;
                right--;
            } else {
                return false;
            }
        }
        return true;
    }
}

代码随想录解法

逻辑一致，注意回溯时s的设置问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
    List<String> result = new ArrayList<>();
    public List<String> restoreIpAddresses(String s) {
        if (s.length() > 12) return result;
        backTracking(s, 0, 0);
        return result;
    }

    private void backTracking(String s, int start, int points){
        if (points == 3){
            if (isValid(s,start,s.length()-1)) {
                result.add(s);
            }
            return;
        }

        for (int i = start; i < s.length(); i++){
            if (isValid(s, start, i)){
                s = s.substring(0, i + 1) + "." + s.substring(i + 1);
                points++;
                backTracking(s, i + 2, points);
                points--;
                s = s.substring(0, i + 1) + s.substring(i + 2);
            } else {
                break;
            }
        }
    }
    private boolean isValid(String s, int left, int right){
        if (left > right) return false;
        if (s.charAt(left) == '0' && left != right) return false;

        int num = 0;
        for (int i = left; i <= right; i++){
            if (s.charAt(i) > '9' || s.charAt(i) < '0') return false;
            num = num * 10 + (s.charAt(i) - '0');

            if (num > 255) return false;
        }

        return true;
    }
}