代码随想录第四十二天

Posted on In

复习

509 斐波那契数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int fib(int n) {
        if (n < 1) return n;
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;

        for (int i = 2; i < n + 1; i++){
            dp[i] = dp[i - 1] + dp[i - 2];
        }

        return dp[n];
    }
}

70 爬楼梯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int climbStairs(int n) {
        if (n <= 1) return n;
        int[] dp = new int[n + 1];
        dp[1] = 1;
        dp[2] = 2;

        for (int i = 3; i < n + 1; i++){
            dp[i] = dp[i - 1] + dp[i - 2];
        }

        return dp[n];
    }
}

746 使用最小花费爬楼梯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        if (n <= 1) return 0;
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 0;

        for (int i = 2; i < n + 1; i++){
            dp[i] = Math.min(dp[i-1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }

        return dp[n];
    }
}

62 不同路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for (int i = 0; i < m; i++){
            dp[i][0] = 1;
        }
        for (int i = 0; i < n; i++){
            dp[0][i] = 1;
        }

        for (int i = 1; i < m; i++){
            for (int j = 1; j < n; j++){
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }

        return dp[m - 1][n - 1];
    }
}

63 不同路径II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];
        for (int i = 0; i < m && obstacleGrid[i][0] != 1; i++){
            dp[i][0] = 1;
        }
        for (int i = 0; i < n && obstacleGrid[0][i] != 1; i++){
            dp[0][i] = 1;
        }

        for (int i = 1; i < m; i++){
            for (int j = 1; j < n; j++){
                if (obstacleGrid[i][j] != 1){
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                }
            }
        }

        return dp[m - 1][n - 1];
    }
}

343 拆分整数

利用 for loop j遍历整个可能

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int integerBreak(int n) {
        int[] dp = new int[n + 1];
        dp[2] = 1;

        for (int i = 3; i < n + 1; i++){
            for (int j = 1; j < i; j++){
                dp[i] = Math.max(dp[i], Math.max(j * (i -j), j * dp[i - j]));
            }
        }

        return dp[n];
    }
}

96 不同的二叉搜索树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;

        for (int i = 2; i < n + 1; i++){
            for (int j = 0; j < i; j++){
                dp[i] += dp[j] * dp[i - j - 1];
            }
        }

        return dp[n];
    }
}

另一种解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n +1];

        dp[0] = 1;

        for (int i = 1; i <= n; i++){
            for (int j = 1; j <= i; j++){
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }

        return dp[n];
    }
}

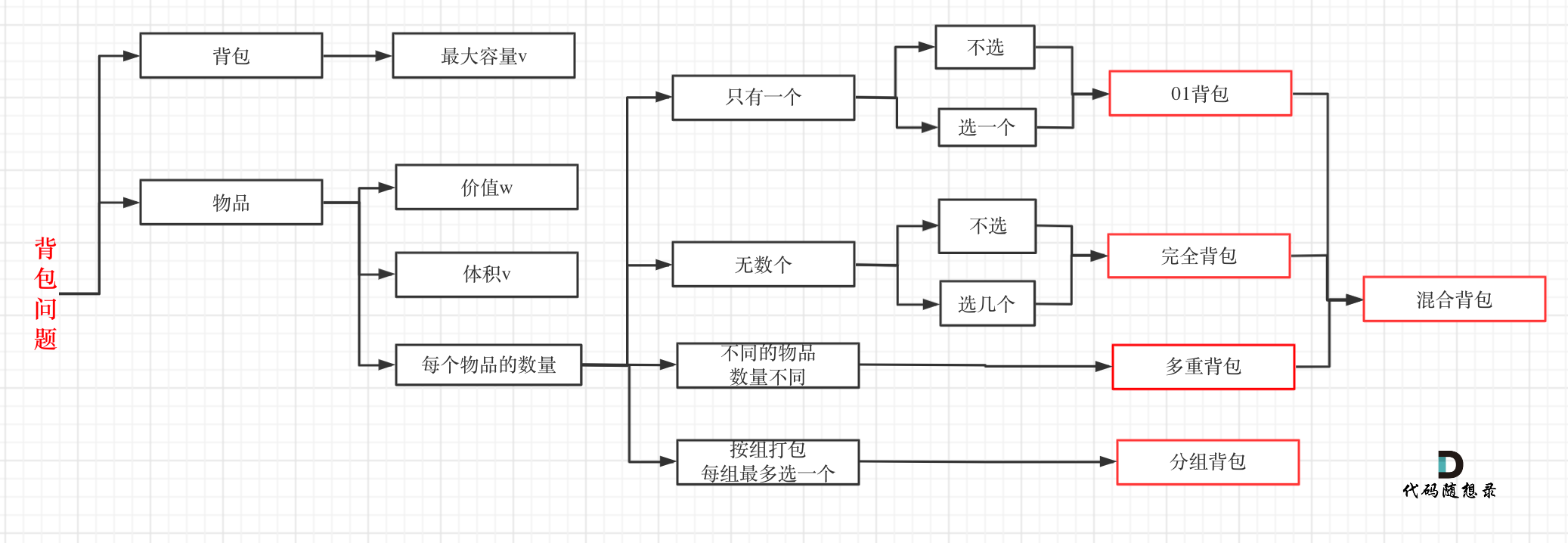
01背包理论基础 二维

需要掌握01背包，完全背包，再加多重背包

01背包问题：
有n件物品，一个最多能背重量为w的背包，第i件物品的重量为weight[i], 得到的价值是value[i]，每件物品只能用一次，求解怎么装物品价值最大

例子：
0 1 15
1 3 20
2 4 30

利用二维dp数组01背包：

  1. 确定dp数组及下标含义
    dp[i][j] 表示从下标为[0-i]的物品任意取，放进容器为j的背包，价值总和最大是多少

  2. 确定递推公式
    有两个方向：
    不放物品i： 由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]
    利用物品的冗余层：
    判断j和weight[i- 1]此时i比物品编号大一
    因为i从1开始
    放物品i：由dp[i - 1][j - weight[i - 1]]推出，dp[i - 1][j - weight[i - 1]] 为背包容量为j - weight[i - 1]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i - 1]] + value[i - 1] （物品i的价值），就是背包放物品i得到的最大价值

  3. 确定初始化
    第一列是0
    第一行大于等于1时，都可以放i

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
import java.util.Arrays;

public class BagProblem {
    public static void main(String[] args) {
        int[] weight = {1,3,4};
        int[] value = {15,20,30};
        int bagSize = 4;
        testWeightBagProblem(weight,value,bagSize);
    }

    /**
     * 初始化 dp 数组做了简化(给物品增加冗余维)。这样初始化dp数组，默认全为0即可。
     * dp[i][j] 表示从下标为[0 - i-1]的物品里任意取，放进容量为j的背包，价值总和最大是多少。
     * 其实是模仿背包重量从 0 开始，背包容量 j 为 0 的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为 0。
     * 可选物品也可以从无开始，也就是没有物品可选，即dp[0][j]，这样无论背包容量为多少，背包价值总和一定为 0。
     * @param weight  物品的重量
     * @param value   物品的价值
     * @param bagSize 背包的容量
     */
    public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){

        // 创建dp数组
        int goods = weight.length;  // 获取物品的数量
        int[][] dp = new int[goods + 1][bagSize + 1];  // 给物品增加冗余维，i = 0 表示没有物品可选

        // 初始化dp数组，默认全为0即可
        // 填充dp数组
        for (int i = 1; i <= goods; i++) {
            for (int j = 1; j <= bagSize; j++) {
                if (j < weight[i - 1]) {  // i - 1 对应物品 i
                    /**
                     * 当前背包的容量都没有当前物品i大的时候，是不放物品i的
                     * 那么前i-1个物品能放下的最大价值就是当前情况的最大价值
                     */
                    dp[i][j] = dp[i - 1][j];
                } else {
                    /**
                     * 当前背包的容量可以放下物品i
                     * 那么此时分两种情况：
                     *    1、不放物品i
                     *    2、放物品i
                     * 比较这两种情况下，哪种背包中物品的最大价值最大
                     */
                    dp[i][j] = Math.max(dp[i - 1][j] , dp[i - 1][j - weight[i - 1]] + value[i - 1]);  // i - 1 对应物品 i
                }
            }
        }

        // 打印dp数组
        for(int[] arr : dp){
            System.out.println(Arrays.toString(arr));
        }
    }
}

简化写法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int[] weight;
int[] value;

int bagSize;
int items = weight.length;
int[][] dp = int[items + 1][bagSize + 1];
for (int i = 1; i < items + 1; i++){
    for (int j = 1; j < bagSize + 1; j++){
        if (j < weight[i - 1]){
            dp[i][j] = dp[i - 1][j];
        } else {
            dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1);
        }
    }
}

return dp[items][bagSize];

动态规划 01背包理论基础（滚动数组）一维

可以把dp[i-1]那一层拷贝到dp[i]上

动态规划五部：

  1. dp数组的意义
    dp[j] 是容量为j的背包，所背的物品的价值最大为dp[j]
  2. 一维dp递推公式
    dp[j]可以通过dp[j - weight[i]]推导出来，dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。

dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上 物品i的价值。

此时dp[j]有两个选择：一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j]，即不放物品i，一个是取dp[j - weight[i]] + value[i]，即放物品i，指定是取最大的，毕竟是求最大价值

即dp[j] = Math.max(dp[j], dp[j - weight[i]] +value[i]);

  1. 一维数组初始化：
    直接所有位置初始为0；
    遍历时j要倒序，因为要保证i只被放进一次，从后面倒序，可以保证不会重复使用一个物品，因为dp从0开始
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public static void main(String[] args) {
    int[] weight = {1, 3, 4};
    int[] value = {15, 20, 30};
    int bagWight = 4;
    testWeightBagProblem(weight, value, bagWight);
}

public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){
    int wLen = weight.length;
    //定义dp数组：dp[j]表示背包容量为j时，能获得的最大价值
    int[] dp = new int[bagWeight + 1];
    //遍历顺序：先遍历物品，再遍历背包容量
    for (int i = 0; i < wLen; i++){
        for (int j = bagWeight; j >= weight[i]; j--){
            dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    //打印dp数组
    for (int j = 0; j <= bagWeight; j++){
        System.out.print(dp[j] + " ");
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
int[] weight;
int[] value;

int bagSize;
int items = weight.length;
int[] dp = int[bagSize + 1];
for (int i = 0; i < items; i++){
    for (int j = bagSize; j >= weight[i]; j--){
        dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

return dp[bagSize];

416 分割等和子集

使用01背包：
N件物品放进最多W的背包，计算value，求解value最大的情况

要求解总和sum/2的子集
背包体积：sum / 2
背包放入的物品的重量和价值皆为 元素的数值
背包如果正好装满，说明找到了总和为2的子集
背包中每一个元素不可重复放入

5部曲：

  1. dp[j] j的最大value
    在本题，dp[j]表示背包总容量是j，放进物品后，背的最大重量是dp[j]
  2. dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
  3. 初始化：题目如果有负数，非0下标就要初始化为-无穷，此题为0
  4. 遍历顺序，j从后向前，i从前向后
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public boolean canPartition(int[] nums) {
        if(nums == null || nums.length == 0) return false;
        int sum = 0;
        for (int i : nums){
            sum += i;
        }

        int n = nums.length;
        if (sum % 2 != 0) return false;
        int[] dp = new int[sum / 2 + 1];

        for (int i = 0; i < n; i++){
            for (int j = sum/2; j >= nums[i]; j--){
                dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
            }

            if (dp[sum/2] == sum/2) return true;
        } 
        return dp[sum/2] == sum/2;
    }
}

每日一题: 49 Group Anagrams

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        Map<String, List<String>> map = new HashMap<>();
        
        for (String i : strs){
            char[] chars = i.toCharArray();
            Arrays.sort(chars);
            String str = new String(chars);
            if (!map.containsKey(str)){
                map.put(str, new ArrayList<>());
            }
            map.get(str).add(i);
        }

        return new ArrayList<List<String>>(map.values());
    }
}